The term standard form was first introduced by Muhammad Al-Khwarizmi in the early 9 th century. He was a Persian mathematician. Scientific notation is another name of standard form, depending on the country in which you live.
In the United States of America, people used the term scientific notation whereas the British people use the conventional word “standard form.” It has different names like normal form, canonical form, etc. Now let’s move forward toward the writing techniques of the standard form.
For decimal, the number that we can write as a decimal number, between 1.0 and 10.0, multiplied by a power of 10, is known as standard form.
What is standard form?
The standard form basically is a method to write a big or very small number in the easiest form by comparing the powers of 10.
Standard form plays a vital role in the calculation it is a method to write a huge amount in a few digits by using a technique commonly used in science and engineering it is similar to scientific notation. For example, consider the speed of light which travels at about 671,000,000 miles per hour. Written in standard form this number is equivalent to 6.71 x 108
Formula of standard form
P × 10n
Where p is a number 1 ≤ p ≤ 9 and n is an integer.
Procedure to form standard form of decimal number
Let’s suppose a number 7,98,000,000
Consider a number 7,98,000,000 to convert it into standard form
by following these steps
Step 1: Write the first digit of the number
Step 2: Write a decimal point after this and also write the remaining non-zero numbers like 7.98
Step 3: Now count the digit after the decimal point and write it in the power of 10.
Step 4: If you are moving in a direction from right to left, then positive power will be used.
Step 5: Thus, standard form of 7,98,000,000 is 7.98 × 108
Steps for Fraction
Fractions are converted into standard form by making numerator and denominator co-prime.
Co-prime numbers
Co-prime numbers are numbers whose common divisor is only one. For example, 5 and 3, 5 and 7, 6 and 11. Moreover, two prime numbers are always co-prime.
Consider the fraction 15/20.
Step 1: Find all the common divisors of the numerator and the denominator first, 15 and 20 have common divisors 1 and 5.
Step 2: Divide the numerator and denominator by 5 because it is greater.
For example:
15 / 20 after dividing the numerator and denominator by 5 it becomes
= 3 / 4
which is the standard fraction and is the standard form of 15 /20
Example Section
In this section with the help of examples, the topic will be described.
Conversion into standard form
1) 0.00000073
2) 58200000000
3) 3296748.39 × 103
Solution:
1. Converting 0.00000073 into standard form
Step 1: Write the number.
= 0.00000073
Step 2: Check the position of the decimal point
= 0.00000073
Step 3: Move the decimal point to the right side of the 1 st non-zero digit that is
= 7.3
Step 4: Now, count the number of digits you have moved and multiply the number with “raise to power 10”. As we have moved the decimal 7 points to the right side.
= 7.3 × 10-7 Answer.
Note: The exponent is negative because we have moved the decimal point toward the right side.
2. Convert 5,82,000,000,00 into standard form.
Step 1: Write the number.
= 58200000000.
Step 2: Check the exact position of the decimal point.
= 58200000000.
Note: If there is no decimal point then it should be on most right side of the number
Step 3: Move the point to the right side of the 1 st non-zero digit that is
= 5.82
Step 4: Now, count the digits you have moved and multiply the number with “raise to power 10”. As we have moved the decimal 10 points to the left side.
= 5.82 × 1010 Answer.
Note: The exponent is positive because we have moved the decimal point toward the left side.
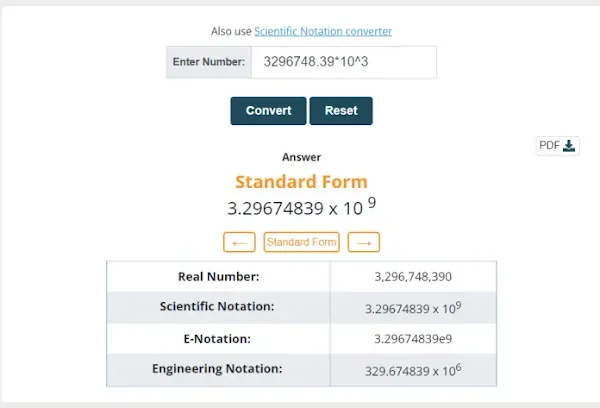
3. Convert 3296748.39 × 103 in standard form.
Step 1: Write the number.
= 3296748.39 × 103
Step 2: Check the position of the decimal point.
= 3296748.39 × 103
Step 3: Move the decimal point to the right side of the 1 st non-zero digit that is
= 3.29674839
Step 4: Now, count the number of digits you have moved and multiply the number with “raise to power 10”. As we have moved the decimal 6 points to the left side.
= 3.29674839 × 103 × 106
= 3.29674839 × 103+6
= 3.29674839 × 109
Which is the standard form of 3296748.39 × 103
The above problems of the standard form can also be evaluated with the help of an online standard form calculator such as:
 |
| Source: https://www.meracalculator.com/math/standard-form.php |
Summary:
In this article, we have studied the basic use of the standard form, its history, and daily life examples. We explained this topic with the help of examples, hope you witnessed that it is not a difficult topic. Now you are able to solve all the basic problems within seconds to make the calculations easier and faster.

